Overview

This demo shows how to create a spaghetti plot of individual-specific effects from a multilevel logistic model.

We will use Ch. 6 data from Bolger & Laurenceau’s Intensive Longitudinal Methods book. In this chapter, the authors used the example of the potential effect of a female partner’s morning anger (amangcw) on her male partner’s report of conflict (pconf; yes/no) later that evening. We will fit a similar model to the model presented in the book, except we will use Bayesian estimation. Using a Bayesian model will allow us to model random slopes.


Read in Data

We will read in the data directly from the Intensive Longitudinal Methods website.

library(data.table)
c <- as.data.frame(
  fread("curl http://www.intensivelongitudinal.com/ch6/ch6R.zip | tar -xf- --to-stdout *categorical.csv")
)

head(c)
##   id time    time7c pconf lpconf    lpconfc     amang     amangc    amangcb
## 1  1    2 -1.875699     0      0 -0.1568773 0.4166667 -0.0697026 -0.4709372
## 2  1    3 -1.727551     0      0 -0.1568773 0.0000000 -0.4863693 -0.4709372
## 3  1    4 -1.579402     0      0 -0.1568773 0.0000000 -0.4863693 -0.4709372
## 4  1    5 -1.431254     0      0 -0.1568773 0.0000000 -0.4863693 -0.4709372
## 5  1    6 -1.283106     1      0 -0.1568773 0.0000000 -0.4863693 -0.4709372
## 6  1    7 -1.134958     0      1  0.8431227 0.0000000 -0.4863693 -0.4709372
##      amangcw
## 1  0.4012346
## 2 -0.0154321
## 3 -0.0154321
## 4 -0.0154321
## 5 -0.0154321
## 6 -0.0154321


Load Libraries

library(brms)
library(ggplot2)
library(dplyr)


Fit Model

catmod1B <- brm(pconf ~ amangcw + amangcb + lpconfc + time7c + 
                (amangcw | id), 
              family = bernoulli, 
              data = c, cores=4) 
summary(catmod1B)
##  Family: bernoulli 
##   Links: mu = logit 
## Formula: pconf ~ amangcw + amangcb + lpconfc + time7c + (amangcw | id) 
##    Data: c (Number of observations: 1345) 
##   Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
##          total post-warmup draws = 4000
## 
## Group-Level Effects: 
## ~id (Number of levels: 61) 
##                        Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS
## sd(Intercept)              0.56      0.13     0.32     0.83 1.00     1507
## sd(amangcw)                0.38      0.19     0.05     0.76 1.00     1085
## cor(Intercept,amangcw)     0.68      0.29    -0.07     0.99 1.00     1557
##                        Tail_ESS
## sd(Intercept)              1955
## sd(amangcw)                1002
## cor(Intercept,amangcw)     1851
## 
## Population-Level Effects: 
##           Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## Intercept    -1.93      0.12    -2.17    -1.71 1.00     2315     2075
## amangcw       0.12      0.12    -0.16     0.33 1.00     2062     1822
## amangcb      -0.23      0.24    -0.71     0.22 1.00     3135     2835
## lpconfc       0.26      0.21    -0.16     0.68 1.00     3332     2750
## time7c       -0.20      0.07    -0.34    -0.05 1.00     4326     2388
## 
## Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
## and Tail_ESS are effective sample size measures, and Rhat is the potential
## scale reduction factor on split chains (at convergence, Rhat = 1).


Generate Predictions


Create a new dataframe

df1 <- dplyr::select(c, id, amang, amangcw, pconf) 
df1$amangcb <- 0
df1$time7c <- 0
df1$lpconfc <- 0


Use new dataframe to generate fitted values

fitdf1 <- cbind(df1, fitted(catmod1B, newdata = df1, re_formula = NULL,  incl_autocor = F))


Obtain the Fixed effect

x <- data.frame(amangc = seq(min(c$amangc), max(c$amangc), by = .1),
                amang = seq(min(c$amang), max(c$amang), by = .1))

x$predM <-(1/(1 + exp(-(fixef(catmod1B)["Intercept", "Estimate"] + 
                          fixef(catmod1B)["amangcw", "Estimate"]*x$amangc))))


Plot the Results


Plot Individual Specific Effects

catspag0 <- ggplot(fitdf1, aes(amang, Estimate, group = id)) + 
  theme_bw() + 
  geom_line() + 
  ylab("Male Report of Conflict") + 
  xlab("Female Morning Anger") +
  scale_y_continuous(breaks = c(0, .5, 1))  
catspag0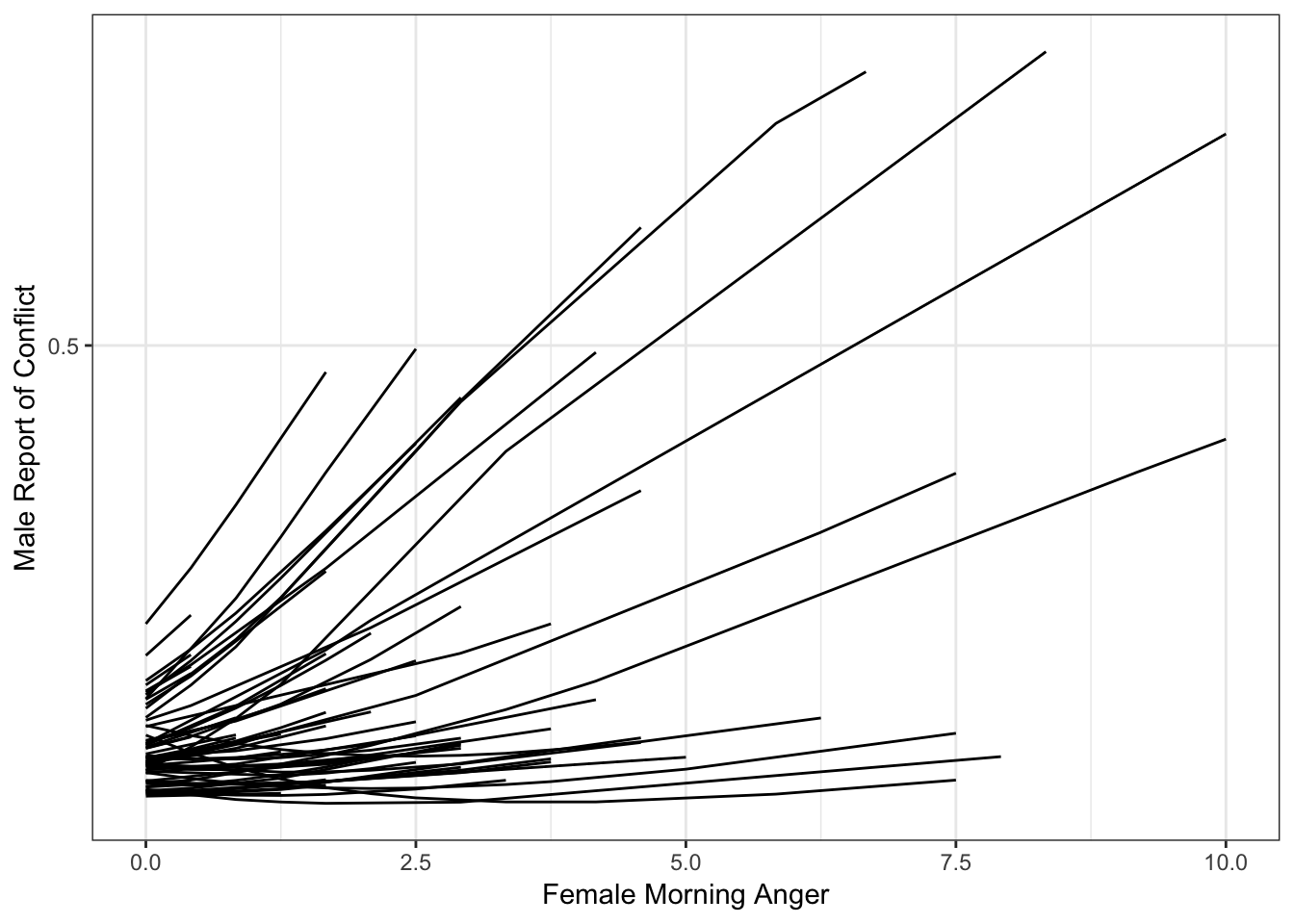


Add in Fixed (Average) Effect

catspag0 + geom_line(data = x, aes(amang, predM, group = NULL), 
            color = "blue",
            size = 2)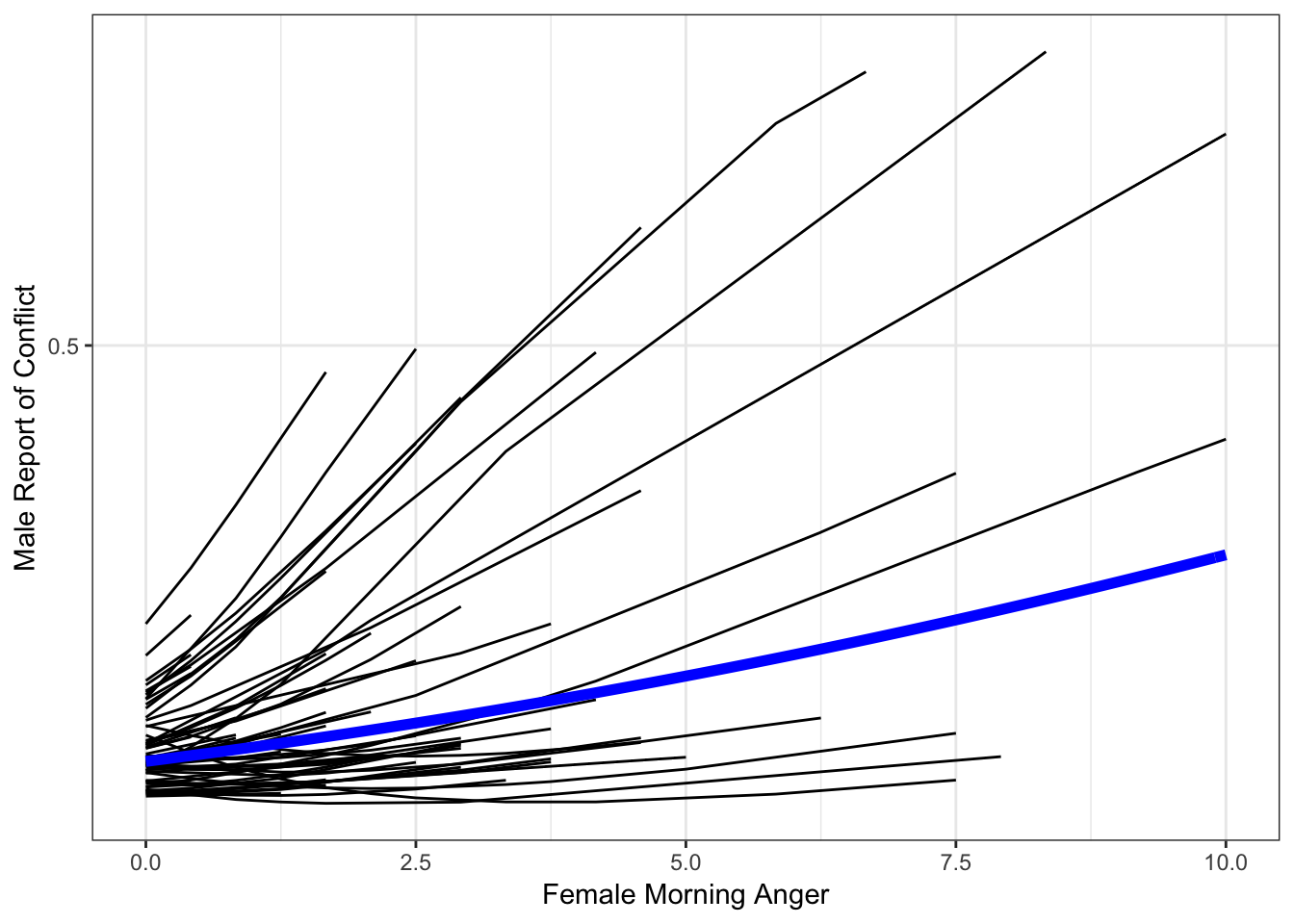


So we have our plot. It’s not bad, but it’s not great either. The individual-specific lines look a bit spikey, and one even looks crooked. We are missing that smooth, sigmoidal shape that characterizes logistic regression effects.

The reason for this is that we need to add more values for each person in order to properly display their effect. As of now, ggplot simply connects the points available, resulting in effects that appear too linear or kinked in some way.


Interpolate Data

To remedy the “spikey” way our spaghetti plot looks, we will need to interpolate data. To be clear, we are NOT adding more data to the model; the model only uses our actual observations to generate estimates. Instead, we are just filling in more datapoints for the purposes of plotting, and we will do this only within each subject’s observed range. In other words, we will not add data that is fall outside of each person’s mininum observed value or maximum observed value.

To accomplish this, we will need to create a new dataframe, called df2. We will begin by setting this dataframe to NULL so that it is just a placeholder waiting to “catch” the data we will populate it with.

Next, we will set up a for loop in which we will ask R to take each subject’s minimum and maximum observed value, and generate values within that range in small increments, in this case increments of .05 (as shown with the seq() function). This will enable us to have a high degree of granularity so that our curves will be smooth when we plot them. We will also need to set other variables to 0, as they were mean centered in our model.

df2 <- NULL
for (i in unique(c$id)) {
  cseq <- data.frame(
  amangcw = seq(min(subset(c, id==i)$amangcw, na.rm=T), 
               max(subset(c, id==i)$amangcw, na.rm=T), .05), 
  amang = seq(min(subset(c, id==i)$amang, na.rm=T), 
               max(subset(c, id==i)$amang, na.rm=T), .05), 
  amangc = seq(min(subset(c, id==i)$amangc, na.rm=T), 
              max(subset(c, id==i)$amangc, na.rm=T), .05), 
  amangcb = 0, 
  lpconfc = 0, 
  time7c = 0, 
  id = i)
  df2 <- rbind(df2, cseq)
}


Now we have a very fine-grained version of our dataframe.

head(df2)
##      amangcw amang     amangc amangcb lpconfc time7c id
## 1 -0.0154321  0.00 -0.4863693       0       0      0  1
## 2  0.0345679  0.05 -0.4363693       0       0      0  1
## 3  0.0845679  0.10 -0.3863693       0       0      0  1
## 4  0.1345679  0.15 -0.3363693       0       0      0  1
## 5  0.1845679  0.20 -0.2863693       0       0      0  1
## 6  0.2345679  0.25 -0.2363693       0       0      0  1


Next, we will use the fitted() function to generate fitted values using this new, fine-grained dataframe. As noted in my Plotting Fixed Effects demo, the brms package that we used to fit our model features both fitted() and predict() to generate model predictions, but these function do slightly different things. We will use fitted() here; however, we would get the same thing using predict() in this case because we are not including uncertainty (i.e., credibility intervals) in these plots.

We will create a new dataframe, cseqpred, in which we will take our new dataframe, interp, and append to it the model predicted values.

fitdf2 <- cbind(df2, fitted(catmod1B, newdata = df2, re_formula=NULL, incl_autocor = F))
head(fitdf2)
##      amangcw amang     amangc amangcb lpconfc time7c id  Estimate  Est.Error
## 1 -0.0154321  0.00 -0.4863693       0       0      0  1 0.1018272 0.03788152
## 2  0.0345679  0.05 -0.4363693       0       0      0  1 0.1019568 0.03875355
## 3  0.0845679  0.10 -0.3863693       0       0      0  1 0.1021133 0.03969056
## 4  0.1345679  0.15 -0.3363693       0       0      0  1 0.1022963 0.04068934
## 5  0.1845679  0.20 -0.2863693       0       0      0  1 0.1025056 0.04174707
## 6  0.2345679  0.25 -0.2363693       0       0      0  1 0.1027410 0.04286125
##         Q2.5     Q97.5
## 1 0.04211750 0.1864994
## 2 0.04077566 0.1891980
## 3 0.03989357 0.1921299
## 4 0.03868077 0.1960297
## 5 0.03765638 0.1993833
## 6 0.03688834 0.2033106


Now, we can create a plot very similar to our prior plot, but we will instead use our more fine-grained dataset so we get that sigmoidal curve we are after.

catspag <- ggplot(fitdf2, aes(amang, Estimate, group = id)) + 
  ylab("Male Report of Conflict") + 
  xlab("Female Morning Anger") +
  theme_bw() +  
  scale_y_continuous(breaks = c(0, .5, 1)) +
  geom_line() + 
  geom_line(data = x, aes(amang, predM, group = NULL), 
            color = "blue",
            size = 2) 
catspag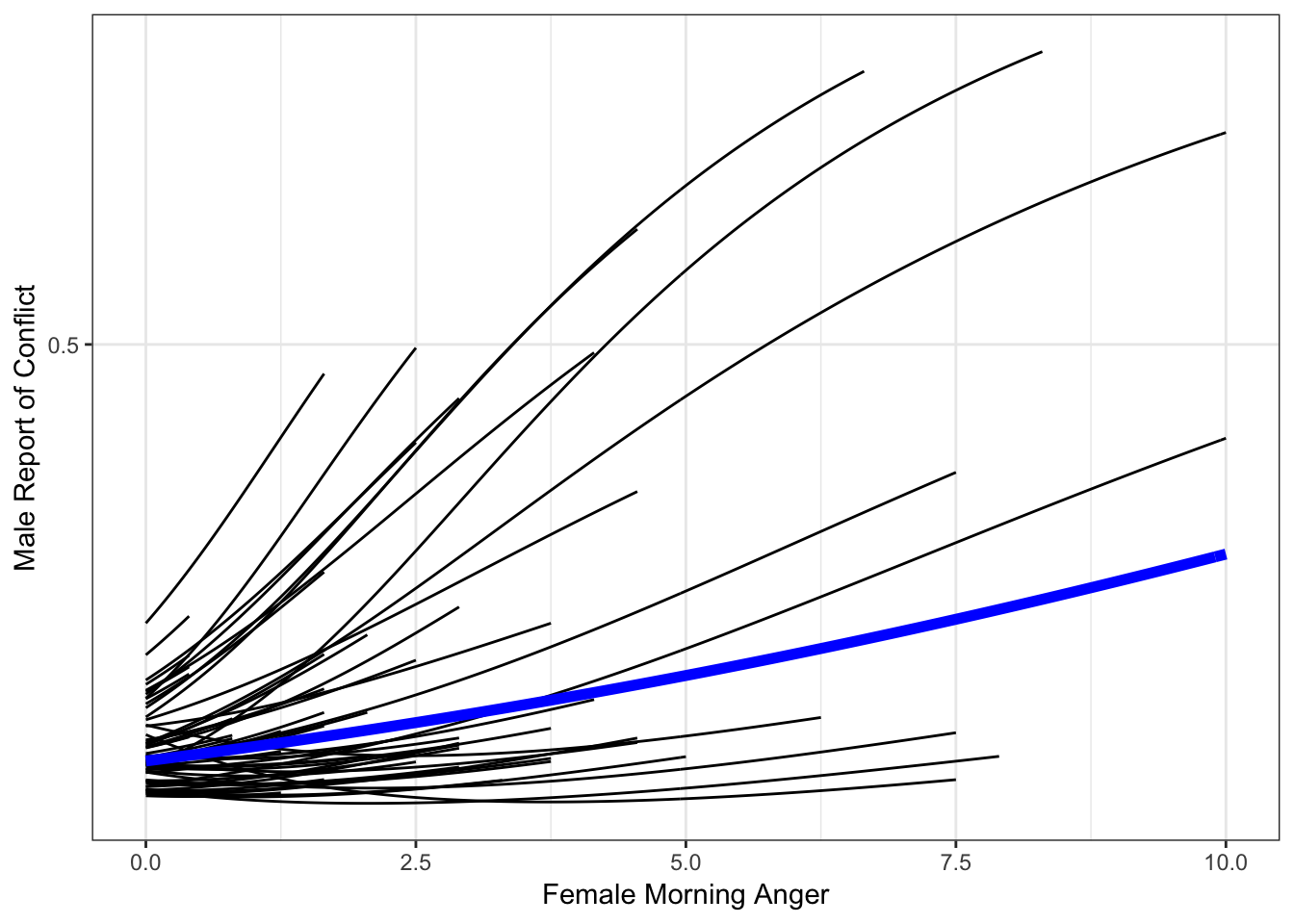


That looks a lot better!


Side by Side Comparison

As a final step, let’s compare these two plots side by side so we can see how using the interpolated data has improved our plot.

library(gridExtra)
grid.arrange(catspag0 + geom_line(data = x, aes(amang, predM, group = NULL), 
            color = "blue",
            size = 2) + labs(title = "Without Interpolated Data"), 
            
            catspag + labs(title = "With Interpolated Data"), ncol = 2)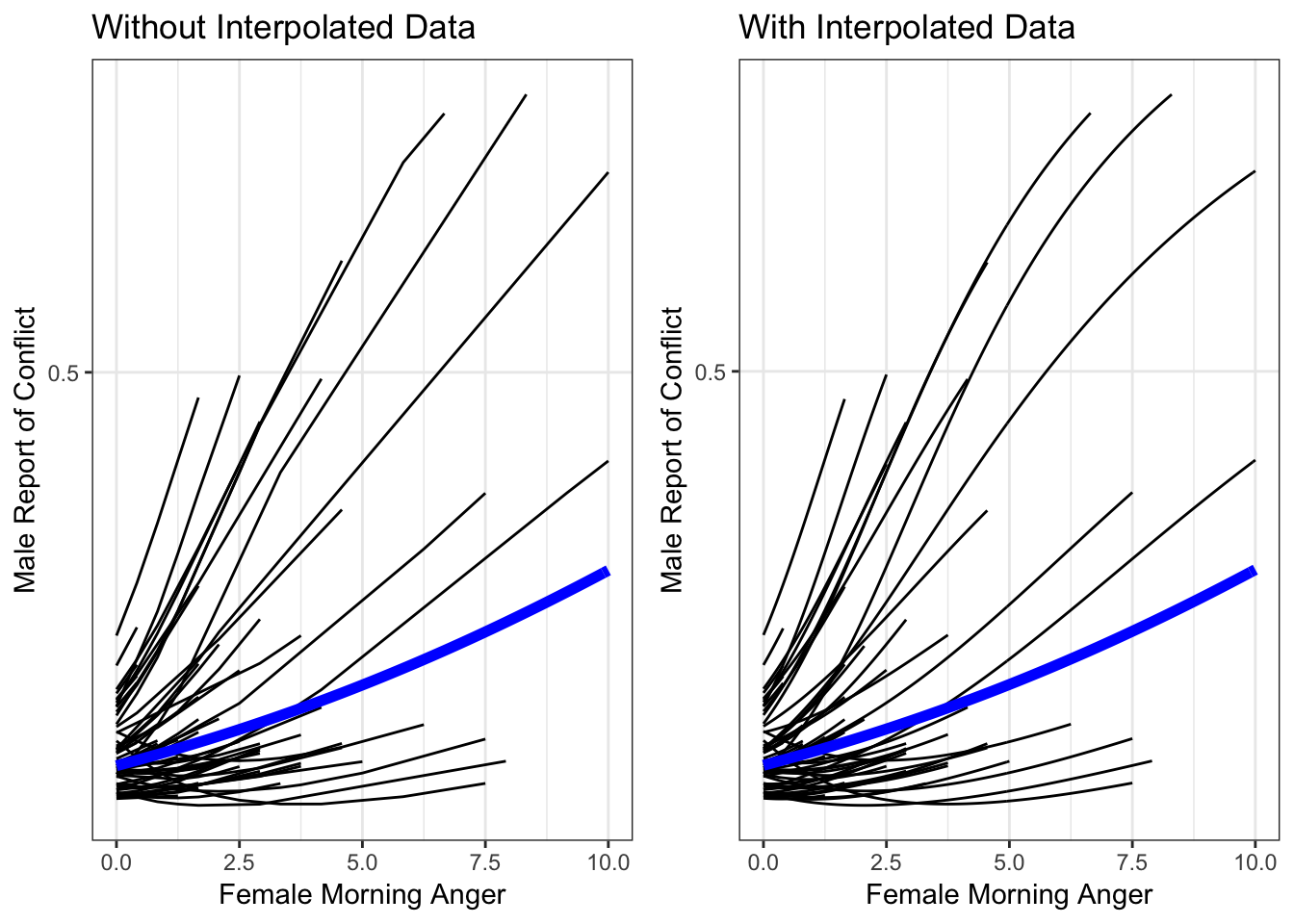


View .Rmd source code

updated April 22, 2019

footer2.knit

 

The material above reflects the best of my knowledge on this topic. Please be sure to check your results and code carefully.